そもそも「ガウス過程」って？
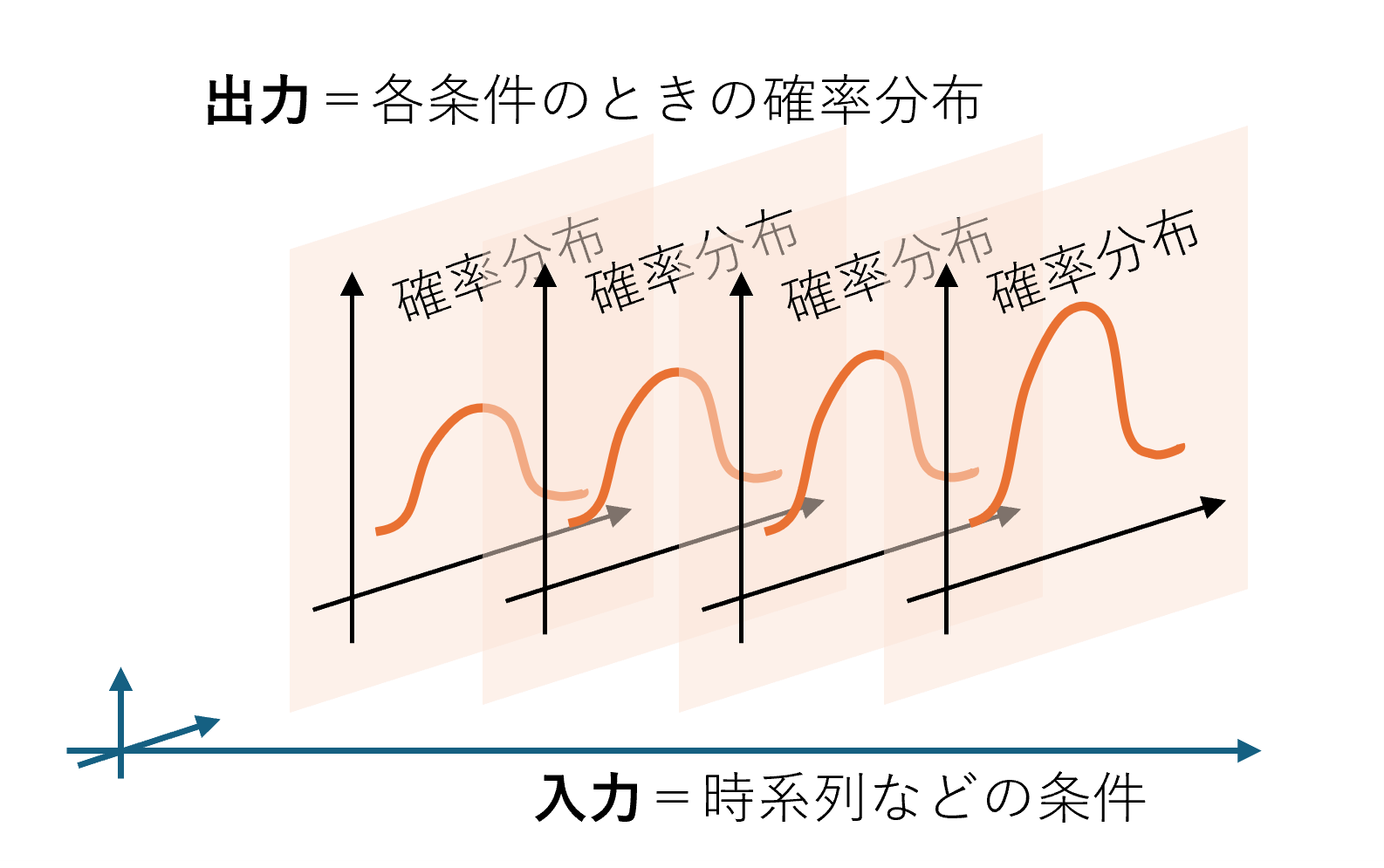
『過程』と聞くと、何かを進めている途中や工程、プロセスを連想するかもしれません。ガウス過程の『過程』は、確率論の専門用語である『確率過程』から来ています。確率過程を調べると、『時間などの条件によって変化する確率変数の数理モデル』と説明されています。これは、時間などの条件（入力）に対して、出力が確率分布となるものを指します。通常の関数では、入力に対して出力が一意に決まりますが、確率過程では出力が確率分布関数となります。さらに、この分布がガウス分布※である場合をガウス過程と呼びます。
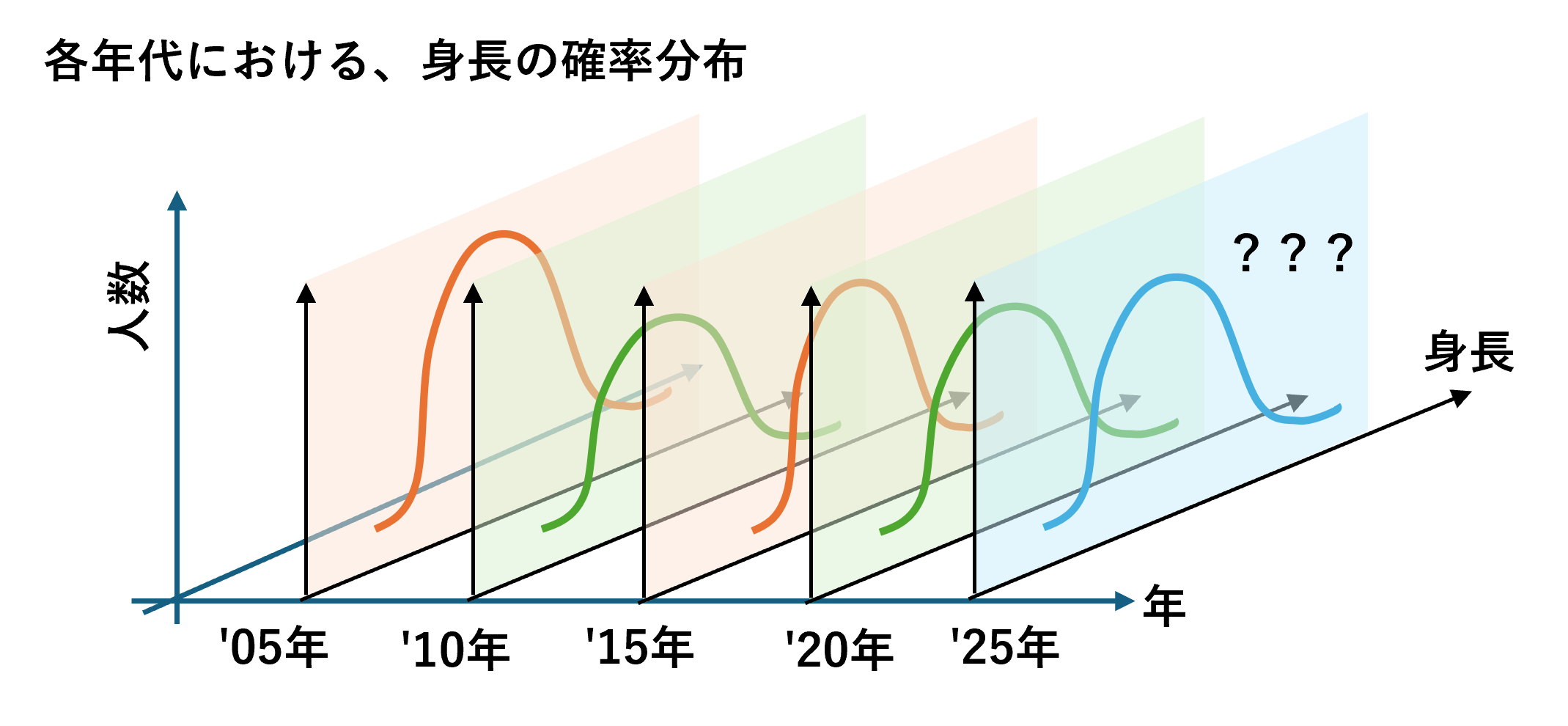
＜例＞ 具体的な例として、ガウス分布でよく知られているものに、身長と人数のグラフがあります。多くの人を集めて横軸に身長、縦軸に人数をとってグラフ化すると、ガウス分布が形成されると言われています。さらに、どの年齢層でもこの分布が成り立つそうです（面白いですね）。各年代のデータを学習させることで、未来の身長の確率分布を予測することが可能なのです。
※ガウス分布とは
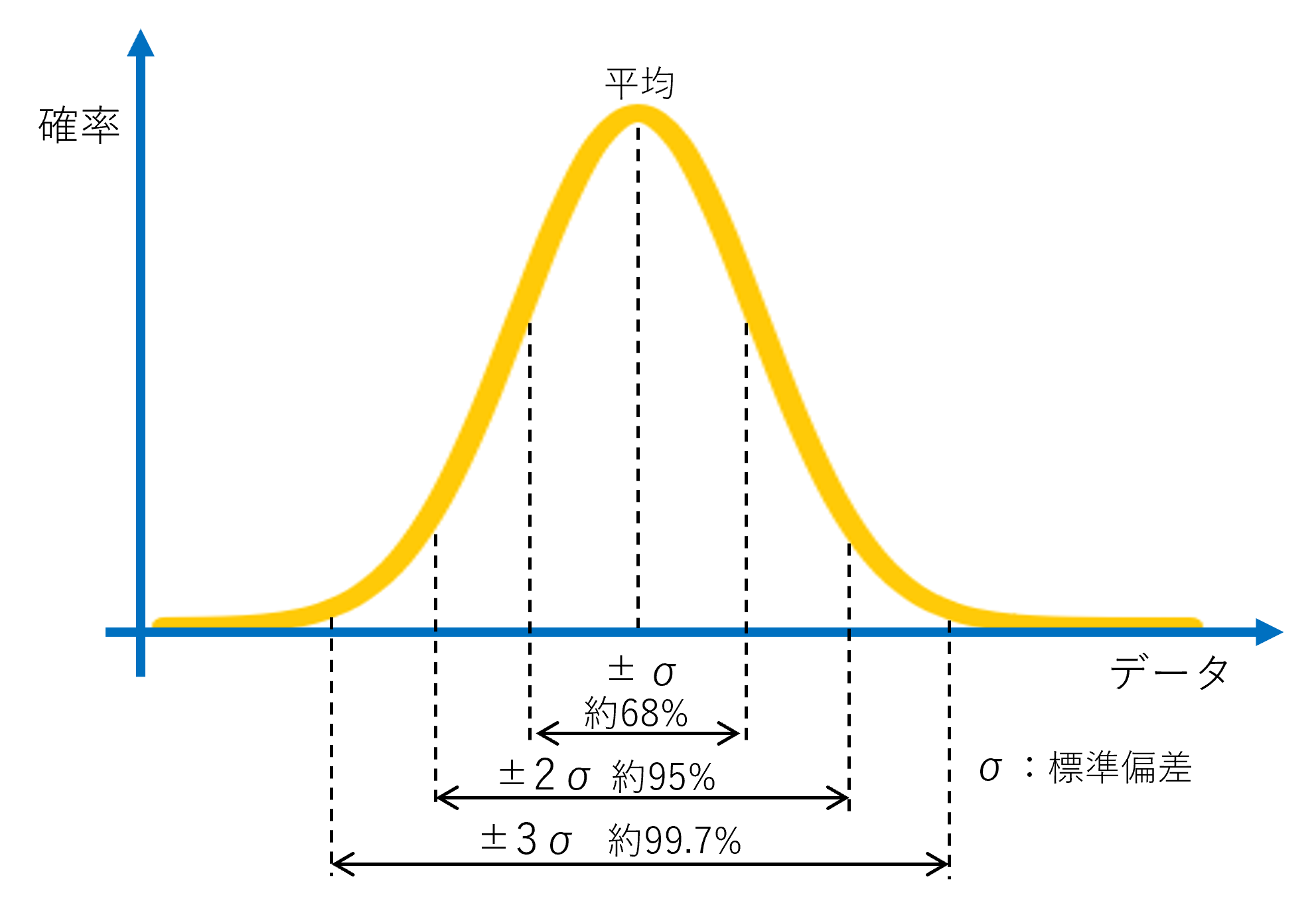
正規分布とも呼ばれ、データがどのように分布しているかを示すものです。横軸にデータ、縦軸に発生確率をとってグラフ化すると、左右対称のベル型の曲線となることが特徴です。ベルの頂点（最も発生確率が高いデータ位置）＝平均値になります。また、ベルの幅がデータのばらつきを表しています。
標準偏差σを用いると、『平均値±σの範囲に、全データの約68%が存在する（σ：標準偏差）』という特徴があり、さらに『±2σの範囲に約95%、±3σの範囲に約99.7%のデータが存在する』となります。この特徴を利用した事例として、不良品の発生確率を測定し、±3σが規定の範囲に入っているかを確認するなど、品質管理に活用されることがあります。
ニューラルネットワークとの違い
機械学習で良く聞くニューラルネットワークと比較すると、ガウス過程には以下のような特徴があります。
①解釈性
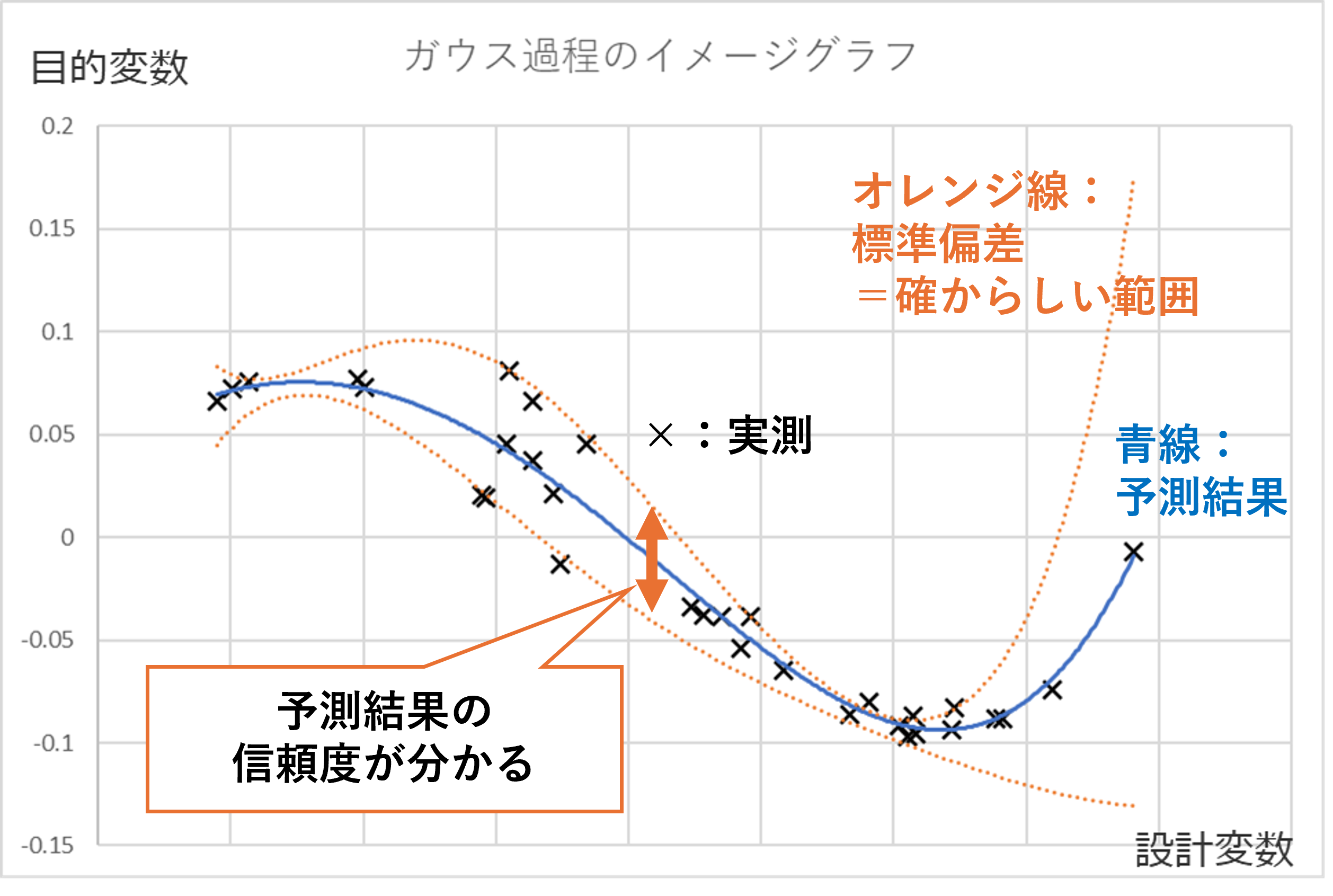
ガウス過程は統計的な数理モデルであり、予測結果に対する不確実性や信頼区間を提供します。そのため、予測された結果が信頼できるかどうか（信頼度）を解釈することができます。
②ケース数
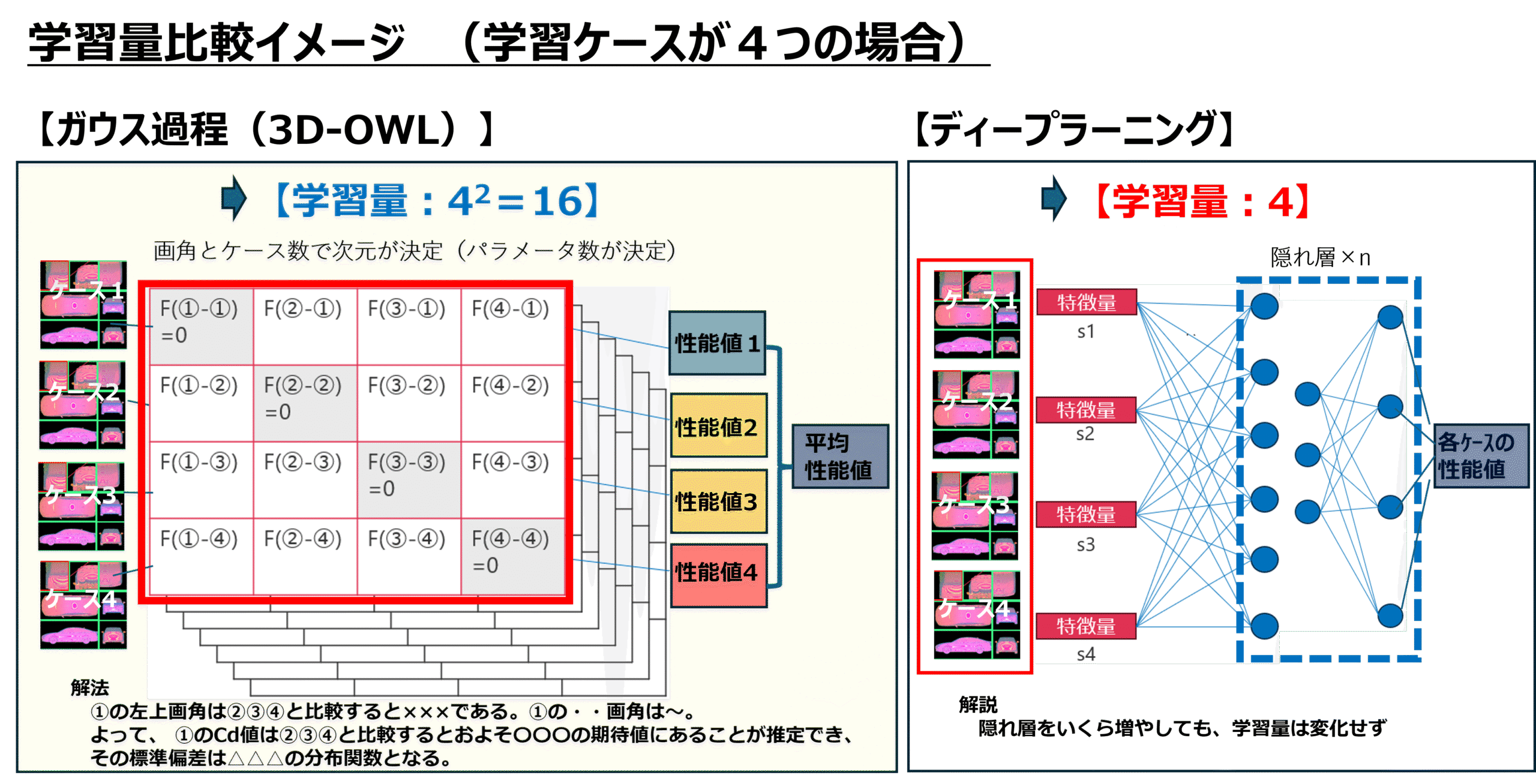
ガウス過程は、少ないケース数でも学習量が多く、比較的早く収束するという特徴があります。少しだけ数学的に言えば、学習量がケース数の二乗に比例して増えます。
一方で、ニューラルネットワークの学習量は一般的にケース数に比例します。そのため、ガウス過程の方が少ないケース数でたくさん学習でき、早く収束
できるのです。逆に言うと、大規模データセットに対してはガウス過程は不向きです。（例えばケース数が数千以上ある場合など）
特許：DepthMapに特化した
独自ガウス過程
3D-OWL®では、DepthMap技術を用いて３次元形状の情報をほとんど損なわずに２次元化し、データ量を非常に軽量化しています。（DepthMapについては別のコラムもぜひご参照ください。） このDepthMapをガウス過程で扱えるようにする、ということが非常に重要な部分であり、東京大学の独自技術を採用しております。（特開2023-054912）
おわりに
トヨタシステムズでは、ガウス過程の特長を最大限に活用し、効果的に3D-OWL®をご利用いただけるよう全力でサポートいたします。
ご質問やご相談はいつでもお待ちしておりますので、お気軽にお問い合わせください！
3D-OWL製品概要はこちら